vSlam | Ibbk

slam-header

In this post, I’ll walk through the creation of a monocular visual SLAM (Simultaneous Localization and Mapping) system using Python, relying on video input from a single camera. The goal is to track the camera’s movement in 3D space while mapping the environment, a crucial part of Autonomous Driving and Robotics

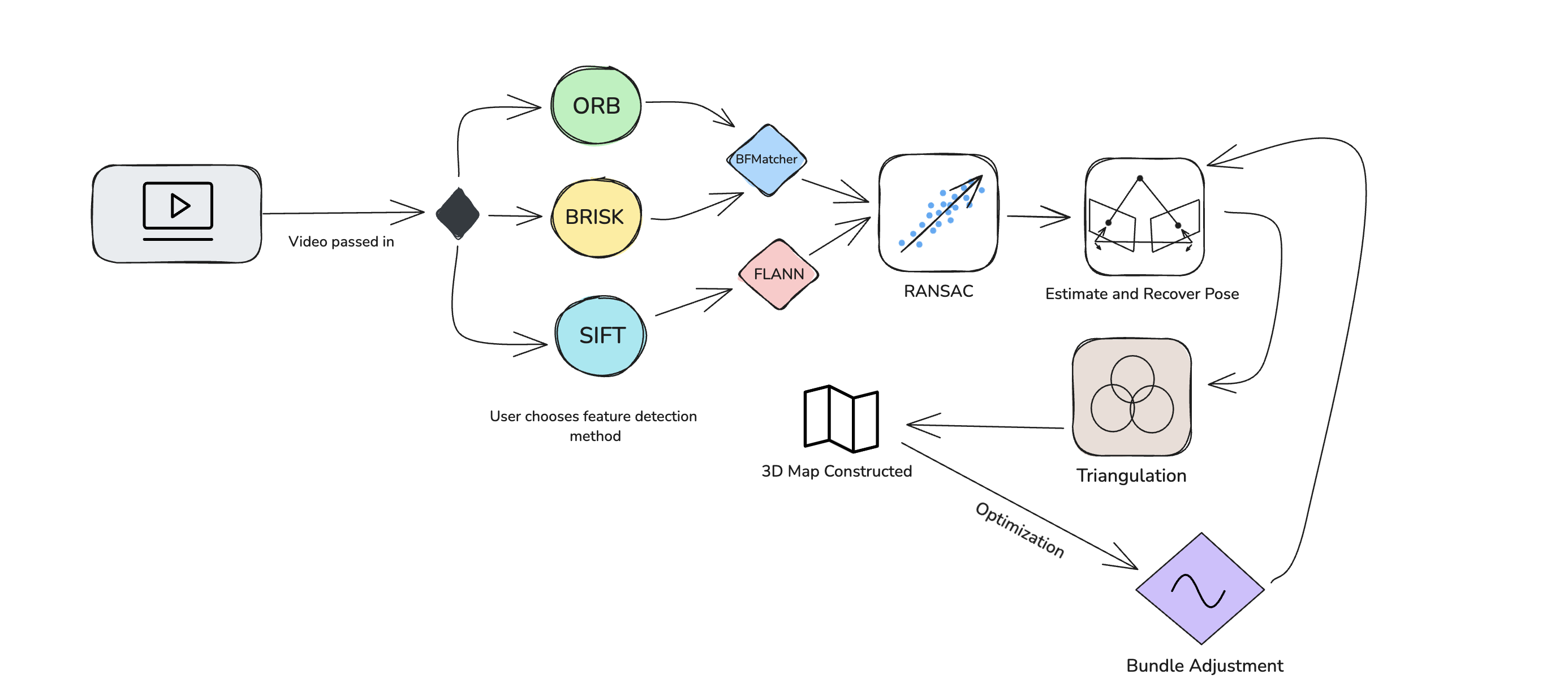
Pipeline

Since we aren’t using any type of radars, we’ll need to rely on vision alone. In practice, this means estimating depth and our position using features between frames. We process the video frame by frame, detect features, match them throughout frames, use this to estimate motion, then use triangulation to create a 3D Map.

Feature Detection

Feature detection is critical because we need to track distinct points across frames. I’ll use algorithms like ORB, SIFT, and BRISK to find and describe these key points in each frame. ORB is faster and works well for real-time applications, while SIFT and BRISK can offer higher accuracy at the cost of speed.

Feature Matching

Once we detect features, we need to match them between consecutive frames. FLANN and BFMatcher are two common techniques for this. FLANN is faster for large datasets, while BFMatcher works well for smaller sets and offers more flexibility in tuning the matching criteria.

Removing Outliers

RANSAC minimizes the number of outliers by fitting a model 𝑀 to the data points 𝑋𝑖 .For an inlier set 𝑆 the error is minimized

\min_M \sum_{i \in S} d(X_i, M)

Where 𝑑(𝑋𝑖, 𝑀) is the distance between the data point 𝑋𝑖 and the model 𝑀.

Pose Estimation

To estimate the camera’s movement, we calculate the essential matrix using the matched points. The essential matrix helps us determine the relative position and orientation of the camera between frames, crucial for tracking its movement in 3D space.

Map Creation

With the camera’s pose estimated, we can use triangulation to pinpoint the 3D coordinates of the matched features. This step is essential for building a 3D map of the environment as the camera moves through it.

Optimization

Bundle adjustment optimizes both the 3D points and the camera parameters by minimizing the reprojection error. For a 3D point 𝑋𝑗 and camera 𝑖 with parameters 𝑃𝑖, the error term is:

e_{ij} = \left\| x_{ij} - P_i X_j \right\|^2

The goal is to minimize the sum of the squared errors across all points and cameras:

\min_{P, X} \sum_{i,j} e_{ij}